September 2020
Good knowledge of financial mathematics is not optional – you need to be able to work the numbers, says top tutor Sunil Bhandari.
Financial mathematics is one of the key skills used in all the financial management/strategy papers set by the professional accountancy bodies. Irrespective of the question style – objective test, paper exam or the new computer-based exam (CBE) – understanding basic
financial mathematics is essential.
The fundamental concept behind financial mathematics is the ‘time
value of money’.
Time value of money
Simply, receiving $1 today is worth more that receiving $1 a year from now. Why? Because:
• You can invest $1 now and earn interest (at r%).
• Inflation means money loses value (purchasing power) with time.
• The $1 received now is risk free, while $1 later may be risky.
Symbols
Here are some commonly used abbreviations in financial mathematics:
PV = Present Value (today at Time 0).
FV = Future Value (as on some specified future date, e.g. Time 1).
r = Cost of Capital (expressed as a decimal, so 10% = 0.10).
n = Number of periods (usually years).
Compound interest
Interest is not just earned on the initial amount invested (the simple
interest approach), but also on the reinvested interest for the period of the
investment. We get ‘interest on interest’ earned in each period. So after ‘n’
interest earning periods:
FV = PV x (1+r)^n
Illustration 1
Assume PV = $500, r = 6% (= 0.06), n = 3 years. What is the equivalent
future value after 3 years?
FV = $500 x (1.06)^3 = $595.51
This formula also links ‘real’ and ‘nominal’ values. In this case, the cost
of capital, ‘r’, is replaced with an inflation rate.
Illustration 2
Real cash flow = $700, Inflation = 5% pa (= 0.05), n = 4 years. What is
the nominal value of the real cash flow after 4 years?
Nominal cash flow = $700 x (1.05)^4 = $850.85
Basic discounting
This is the reverse of compounding. When given the FV, it can be
converted back to its PV by applying the relevant discount factor.
PV = FV x (1+r)^(-n)
Illustration 3
FV = $595.51, r = 6% (= 0.06), n = 3 years. What is the equivalent present value?
PV = $595.51 x (1.06)^(-3) = $595.51 x 0.840 = $500
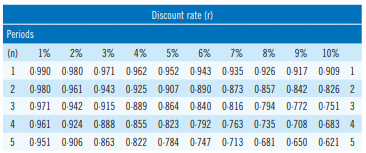
The ‘(1+r)^(-n)‘ is called the discount factor. The exam will provide you
with a discount factor table. (r = 1% to 20% and n = 1 to 15).
If you a sitting ACCA FM, or the new ACCA AFM CBE, the ‘spreadsheet’ response area makes calculating multiple discount factors straightforward.
Head up your spreadsheet with a row containing the number of each year, e.g. 1, 2, 3, and 4. Enter ‘(1+r)^(-n)’, referencing the ‘n’ to the cell containing 1. Then ‘copy & paste’ this formula across the page. Then multiply your cash flows by these discount factors. Alternatively, use the = NPV function directly.
Annuity discount factor
An annuity is defined as an annual cash flow that commences in one year’s time and continues for a defined period.
Illustration 4
Cash Flow for 1 -3 = $500pa, r = 10% (=0.10).
Using the basic discount factors (DFn), this could be presented as:
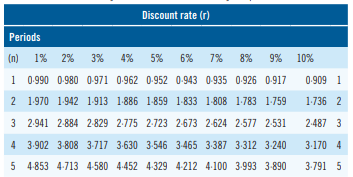
PV = (500 x DF1) + (500 x DF2) +(500 x DF3)
Which is the same as PV = 500 x (DF1 + DF2 + DF3)
If we use the basic discount table shown above:
PV = 500 x (0.909+0.826+0.751) = 500 x 2.486 = $1,243
Here, 2.486 is known as the annuity discount factor, or cumulative discount factor. This can be calculated directly using this formula:
AF (n years, r%) = 1-(1+r) -n
_________
r
Or (1 – (1 + r)^(-n))/r
So AF (3 years, 10%) = (1-(1+0.10)^(-3))/0.10 = 2.487
(note the small rounding difference)
In this case the annuity discount tables are very helpful!
A cautionary note: many candidates make this common error:
PV = (3 x 500) x 2.487 = $3,731.
In ACCA FM and CIMA F3, this answer will be a distractor answer!
Perpetuity discount factor (or perpetual annuity discount factor)
A perpetuity is a series of same value cash flows.
A growing perpetuity is a series of cash flows growing each period by a set %, g%.
The discount factor for a growing perpetuity = 1/(r – g)
Notice 2 things:
- The first cash flow in the series is at time 1, but the value is at time 0.
- If the perpetuity is not growing (g = 0), the discount factor = 1/r
Illustration 5
Perpetual annual cash flow starting at time 1 = $800 pa, r = 9%
(= 0.09)
PV =$800 x 1/0.09 = $800 x 11.111 = $8,889
Illustration 6
Growing perpetual annual cash flow starting at time 1 = $800,
r = 9% (=0.09), g = 3% (= 0.03) each year (=’per annum’, or pa)
PV = $800 x 1/(0.09 – 0.03) = $800 x 16.667 = $13,333
Advanced and delayed annuities and perpetuities
Annuities and perpetuities that start at time 0 have a simple rule: ADD 1!
Illustration 7
Cash Flow for 0 – 3 = $500pa, r = 10%
PV = PV = 500 x (1+ AF 1-2)
PV = PV = 500 x (1+ 1.736) = $1,368
Delayed annuities and perpetuities
Can be valued either:
a) by discounting a simple annuity/ perpetuity, or as
b) a simple annuity/perpetuity, less the value of the missing cash flows
Illustration 8
Perpetual annual cash flow starting from time 4 of $800 pa, r = 9%
a) CF x (1/r x DF the year before the annuity commences)
= $800 x (1/r x DF3) = $800 x (1/0.09 x 0.772) = $6,862
b) CF x (1/r – AF(3 years, 9%)) = $800 x (1/0.09 – 2.531) = $6,864
(rounding difference excepted).
• Sunil Bhandari is an ACCA FM and AFM and CIMA F3 Tutor with FME Learn Online. See www.SunilBhandari.com